In the last blog, we were introduced to the concept and were given an overview of the different steps required in building a Neural Network. In this blog we will learn in detail about the first few steps required to build the neural network.
When we build the Neural Network, one of the choices we get to make is what Activation Function is to be used for the hidden layers. Before we move on to what Activation Functions are, let us refresh our brains on how the Neural Networks operate. They take in the input parameters with the associated weights and biases and then computes the output sum on the "activated" neurons.
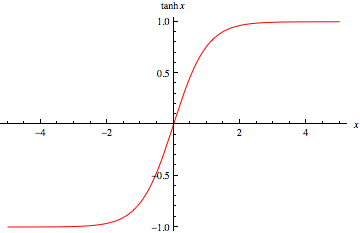
In the last blog we used the sigmoid activation function, but the activation function that almost always works better than the sigmoid function is the Hyperbolic Tangent Function.
The tanh function is defined as:


When we build the Neural Network, one of the choices we get to make is what Activation Function is to be used for the hidden layers. Before we move on to what Activation Functions are, let us refresh our brains on how the Neural Networks operate. They take in the input parameters with the associated weights and biases and then computes the output sum on the "activated" neurons.
In the last blog we used the sigmoid activation function, but the activation function that almost always works better than the sigmoid function is the Hyperbolic Tangent Function.
The tanh function is defined as:
a(z)=tanh(z)=(e^z + e^-z)/(e^z - e^-z) ; where -1≤a(z)≤1

This function is almost always better than the sigmoid function because it ranges over values between -1 and 1, which means that the mean of the activation function will be closer to 0. When we kind of center our data to a 0 mean using a tanh function, it has an effect of actually making the learning for the next layer a little bit easier.
We have another activation function which is nowadays increasingly becoming the default choice of deep learning models, is the ReLU or the Rectified Linear Unit. This function is defined as:
a(z)=max(0,z)
The ReLU function solves the vanishing gradient problem, i.e. the gradient of the sigmoid and the tanh function is very small and close to 0, and hence vanishes but the gradient in the ReLU function is either 0 or 1, and hence can never vanish. And also since this is a non-linear function, which means that we can easily backpropagate the errors and is also less computationally expensive since it involves only a simple mathematical operation. The derivative of the ReLU function at 0 is technically not definable, but when we implement it on the computer, the derivative results to be a very small value. So while practice, we can take the derivative at 0 to be either 0 or 1, and the result is approximately correct for both the cases.
This function suffers from a dying ReLU problem , i.e., for z<0, the gradient will be 0, which means that the weights of the corresponding neurons will not be adjusted and the neuron will stop responding resulting to a dead neuron. So, to counter the dying neuron problem, we use a modified version of the function called the Leaky ReLU Function.
In the Leaky ReLU function, we take the z<0 values, which form the y=0 line and convert it into a non-horizontal straight line by adding a gradient α, where α=0.01.
These are the most common Activation Functions used in Deep Learning Models. There is no hard and fast rule for selecting a particular activation function. The selection depends on the model's architecture, the hyperparameters and the features we are attempting to capture. In the upcoming blog, we will dig deep into the mathematical approach of the forward and backward propagation.
Comments
Post a Comment